https://opensource.com/article/17/9/introduction-machine-learning

Machine learning and artificial intelligence have changed a lot since the last wave of interest, about 25 years ago.

Image by :
opensource.com
Machine
learning and artificial intelligence (ML/AI) mean different things to
different people, but the newest approaches have one thing in common:
They are based on the idea that a program's output should be created
mostly automatically from a high-dimensional and possibly huge dataset,
with minimal or no intervention or guidance from a human. Open source
tools are used in a variety of machine learning and artificial
intelligence projects. In this article, I'll provide an overview of the
state of machine learning today.
In the past, AI programs usually were explicitly programmed to perform tasks. In most cases, the machine's "learning" consisted of adjusting a few parameters, guiding the fixed implementation to add facts to a collection of other facts (a knowledge database), then (efficiently) searching the knowledge database for a solution to a problem, in the form of a path of many small steps from one known solution to the next. In some cases, the database wouldn't need to or couldn't be explicitly stored and therefore had to be rebuilt.
One example is an object/scene manipulation, such as "take the red stone and put it on top of the yellow stone" that incorporates implicit information (e.g., that the red stone is under the blue one). The possible transformations of this world are given; it's up to the AI program to find a solution to get from the start to the end. Another example is steering a car. The AI is given specific boundary conditions, and possible actions (steering, braking, accelerating) are expressed. For a given action, there's a start position, an end position, and boundary conditions, and it's up to the AI to handle it. For example: "Turn 90 degrees to the right, end 50 meters forward and to the right, do not drive more than 15km/h, and do not decelerate more than 10m/s2."
These are search and optimization problems, and solving them is not necessarily AI or a learning program. The core part of learning—and what makes it interesting—is that if there is a set of rules, they are numerous. But sometimes no rules exist, and it's just a matter of whether the program's individual steps are possible and useful. These types of problems cannot really be solved with old-style AI programs.
This is all quite abstract, so let's look at examples.
A statistical approach could use a large number of (simple) functions with an even larger number of variables. The inputs to the functions can be numerous—maybe the value of every single pixel in a picture. The task would be to determine the appropriate values for all the variables to ensure that interpretation of the results of all the functions matches the tags given.
With this approach, no one has to understand the internal rules for the intermediate states and how to get from one state to the next. The only thing that counts is that the result is correct and that an algorithm can be designed to efficiently adjust the internal variables appropriately.
On the other hand, the same statistics that let a human devise a rule (such as, "if 'manifold' and 'tensor' are used in the same document, the topic might be theoretical physics") can be used by a machine to the nth degree; i.e., instead of looking just for a few hopefully relevant and stand-out words, a large (or huge) number of such rules can be used—as long as no one has to explicitly create the rules. Plus, if everything is automatic, there is no reason to stop with words; you could also look for phrases or word sequences, as well as to automatically recognize and filter the most common words.
A modern approach would require much less upfront information. It would just need a function that evaluates the current situation, then determines whether it is better or worse than the previous situation. For instance, the simulated search might have the searcher go from one location to the next, but this might mean leaving the search area or determining that it's not doable or practical because of limitations (e.g., the terrain is too steep). This kind of differential information is usually much easier to come by than evaluating the entire scenario for a global planning algorithm. A local evaluation function can create an algorithm that, over many iterations, finds the destination without explicitly being told how to—or even about the rules of the world.
During the last big surge of interest in AI, 25 to 30 years ago, we didn't have the computing power, size, or complexity available today, so these methods were impossible. The increase in model complexity has made the difference that's allowed problems to be solved with (what appears to be) intuition and superhuman power.
Today we can throw a problem at an algorithm and, given sufficient data, get a result after hundreds, thousands, or even millions of computer hours. Whether or not the result is usable is another question, which brings us to one of the most important points.
Although the new approach offers solutions to problems that previously were too complex to consider or wouldn't have justified the high development cost, now we must critically evaluate the value of each model. Not just once, but regularly and repeatedly during the entire lifetime of the model, because the input data might imperceptibly change from useful to garbage (with corresponding garbage results).
In some situations, there might not be a sufficient model. Maybe the task is simply impossible, or no input data is provided, or the model does not have enough degrees of freedom to represent all the nuances. The algorithms to produce the models will usually terminate and present a result. Whether the model is useful must be determined afterwards.
The selection of a model's statistics and parameters is like creating a hypothesis. Most methods have a few parameters that can be freely and independently chosen, creating a possibly unlimited search space. On the other hand, there's a lot of compute power, and there's a finite number of methods that could test many different models at the same time.
Input data must be collected ahead of time for two purposes:
First, the training data is applied to the model. If each input dataset record is associated with an expected result, we talk about a supervised learning problem, in which we try to discover a function that allows a target value to be computed from a set of input values that can be measured about an entity. (The measured data is the "input dataset record," and the target is the expected result.) If the output value is one of a given set, we talk about a classification problem. If the output is real-valued, we look at a regression problem. Otherwise it is unsupervised, meaning we have data and no specific goal or target.
After the model is trained, then it must be validated with the testing data. The model is applied to the inputs from the training dataset. In the case of a supervised learning problem, the results are compared with the available results from the testing set, and the match is measured. In the case of an unsupervised method, we must find other ways to evaluate the "correctness" of the model.
In the end, we get a score for the current model predicated on the currently available dataset. Then we can decide whether the model is good enough and we can use it (we call this inference) or whether to start again and develop a new model, perhaps with new parameters.
In addition, it's unrealistic to expect a model to find a 100% match with the observed data. There are just too many limitations in place, such as:
Other limitations include:
At a similar level of intuitiveness are algorithms to look for similarities. Given that we can measure the "distance" between two datasets, we can use the k-nearest neighbor (kNN) method to cluster similar dataset records together. The algorithm does not need to know how many clusters we are looking for, and it works (though it's more unstable) with high-dimensional data. This is an unsupervised method and does not require any value to be computed from the input data. The input dataset is the data that's used.
Decision trees are also simple to use and interpret. They are mostly useful for classification problems, but with some limitations, could be used for regression as well. They work by splitting the remaining set of inputs into two pieces at every step along one dimension of the value. Afterwards, ideally one or both sides of the split contain only values of the same class (only cats, only dogs, only pudding). If this is not possible, at least the sets of data points on each side of the split are more "pure."
The process is repeated until the sets are pure (trivially possible if the set has just one element) or the resulting tree exceeds a depth limit. The resulting model is used by testing a new data element according to each split, down to the leaf of the tree, then it adopts as the answer the majority result of the remaining set in that leaf. Such a model can be easily translated into human languages as a cascade of if-then-else statements.
Inference using NNs is simple: the input is applied as a vector. There is a possibly large set of internal "neuron layers," which receive their inputs from the previous layer (or the inputs), and produce results for the next layer (or the output). Each neuron can take all or a subset of the values from the previous layer, scale each value with a factor, and then add up all the values. Then a constant value is added to make the method more general.
This operation can be expressed as simple vector-matrix multiplication. Performing all the operations for a layer at once is a tensor multiplication. The resulting scalar value is then optionally applied to a function that tries to create a binary output (0/1 or 1/-1). The sigmoid or ArcTanh functions are usually used. Repeat the process until the end, when a custom method can be used to determine the result from the output value or values of the last layer. NNs are particularly good at classification, but can be used for regression too.
The tricky part is how to construct the matrices representing the steps from one layer to the next. We have many input dataset records for which NNs can be evaluated. Maybe we could even compute a constellation of the matrices that would result in the exact right value for one input dataset record. But this computation would most likely invalidate similar steps we had done to match other records. There is no closed formula to compute the right values. A gradual learning approach is needed, where all dataset records are looked at repeatedly, each time the difference from the expected result is computed, and then a small step toward correcting the mistake is made (via a method called gradient descent).
We've created many variants of NNs that are good at different tasks. Convolutional NNs (CNNs) are good at handling pictures. Convolution can isolate features, regardless of their position or even orientation. Whether the cat is in the lower right or upper left part of the picture does not matter to a CNN.
Recurring NNs (RNNs) are good for temporal problems. Predicting time series (and anomaly detection), simulating long term vs. short term memory, and similar tasks can be implemented with RNNs.
Independent from these broad categories are methods to improve learning speed, improve the scale of problems that can be solved, or speed the time to train the system. For the latter, there are ways to construct NNs so they don't require tagged training data and become unsupervised algorithms.
Companies like Google, Facebook, LinkedIn, and Amazon have built their business models on these algorithms.
Convex optimization problems are straightforward search problems. Implementations differ in speed and in the requirements on the data provided, but, by definition, they are able to find the solution. Non-convex optimization problems can be solved probabilistically; this is perhaps where the confusion comes from. Nevertheless, optimizations are different from AI/ML. They are prevalent in the business world and most of those problems likely can be solved by optimization.
How are you using open source tools in your machine learning or AI projects? Send an article proposal to open@opensource.com.
In the past, AI programs usually were explicitly programmed to perform tasks. In most cases, the machine's "learning" consisted of adjusting a few parameters, guiding the fixed implementation to add facts to a collection of other facts (a knowledge database), then (efficiently) searching the knowledge database for a solution to a problem, in the form of a path of many small steps from one known solution to the next. In some cases, the database wouldn't need to or couldn't be explicitly stored and therefore had to be rebuilt.
One example is an object/scene manipulation, such as "take the red stone and put it on top of the yellow stone" that incorporates implicit information (e.g., that the red stone is under the blue one). The possible transformations of this world are given; it's up to the AI program to find a solution to get from the start to the end. Another example is steering a car. The AI is given specific boundary conditions, and possible actions (steering, braking, accelerating) are expressed. For a given action, there's a start position, an end position, and boundary conditions, and it's up to the AI to handle it. For example: "Turn 90 degrees to the right, end 50 meters forward and to the right, do not drive more than 15km/h, and do not decelerate more than 10m/s2."
These are search and optimization problems, and solving them is not necessarily AI or a learning program. The core part of learning—and what makes it interesting—is that if there is a set of rules, they are numerous. But sometimes no rules exist, and it's just a matter of whether the program's individual steps are possible and useful. These types of problems cannot really be solved with old-style AI programs.
The new approach
Instead of relying on a huge set of rules, the new approach to ML/AI is to provide a start state, based on the universe in which the problem exists, and the specific goal (if one exists), then let the learning process figure out the intermediate states and how to progress from one state to the next. The internal states and transitions (which we call a model) are developed with the help of statistics. (As an aside, I'd suggest that a better name for today's ML/AI is statistical learning.) The more complicated the problem, the more (internal) variables the formulation has.This is all quite abstract, so let's look at examples.
Example 1: A collection of pictures is tagged with cat, dog, or pudding. After a learning phase, the program is expected to correctly classify pictures it has not seen before.It is hard to design an algorithm that would extract features from a picture to serve as input for a search algorithm. It is logistically impossible to design and implement by hand more than a few dozen features, and those might not be sufficient.
A statistical approach could use a large number of (simple) functions with an even larger number of variables. The inputs to the functions can be numerous—maybe the value of every single pixel in a picture. The task would be to determine the appropriate values for all the variables to ensure that interpretation of the results of all the functions matches the tags given.
With this approach, no one has to understand the internal rules for the intermediate states and how to get from one state to the next. The only thing that counts is that the result is correct and that an algorithm can be designed to efficiently adjust the internal variables appropriately.
Example 2: From a large number of documents, texts about related topics are grouped together.Training such a program might begin with extracting individual words, as the assumption is that texts about a similar topic share a common vocabulary. Perhaps the sentence structure could be examined and the nouns might suggest connections. But what about texts that have no distinct vocabulary? Or incomplete sentence structure? Or are written in different languages? Writing expert text-understanding algorithms is simply not scalable.
On the other hand, the same statistics that let a human devise a rule (such as, "if 'manifold' and 'tensor' are used in the same document, the topic might be theoretical physics") can be used by a machine to the nth degree; i.e., instead of looking just for a few hopefully relevant and stand-out words, a large (or huge) number of such rules can be used—as long as no one has to explicitly create the rules. Plus, if everything is automatic, there is no reason to stop with words; you could also look for phrases or word sequences, as well as to automatically recognize and filter the most common words.
Example 3: To navigate an unknown area, an algorithm efficiently creates a search plan that eventually covers the entire area to locate a specific destination.Such a plan would have to handle unforeseen obstacles such as walls, impassable terrain, etc., as they are navigated. Therefore, there can't be one static plan; rather it must be revised every time new information is available. The program might not even have an answer for situations the code was not programmed to handle.
A modern approach would require much less upfront information. It would just need a function that evaluates the current situation, then determines whether it is better or worse than the previous situation. For instance, the simulated search might have the searcher go from one location to the next, but this might mean leaving the search area or determining that it's not doable or practical because of limitations (e.g., the terrain is too steep). This kind of differential information is usually much easier to come by than evaluating the entire scenario for a global planning algorithm. A local evaluation function can create an algorithm that, over many iterations, finds the destination without explicitly being told how to—or even about the rules of the world.
Let the computer do it
What these examples have in common—what the new approach to machine learning is about and why this hasn't been done before—is that the computer does a lot of work. Instead of immediately honing on a solution, it must take many minute steps, even steps in the wrong direction. If done correctly, a huge number of repetitions will eventually help identify a solution.During the last big surge of interest in AI, 25 to 30 years ago, we didn't have the computing power, size, or complexity available today, so these methods were impossible. The increase in model complexity has made the difference that's allowed problems to be solved with (what appears to be) intuition and superhuman power.
Today we can throw a problem at an algorithm and, given sufficient data, get a result after hundreds, thousands, or even millions of computer hours. Whether or not the result is usable is another question, which brings us to one of the most important points.
Beware of the results
All the new approaches depend on statistics. Basically, we have functions that take input data and produce one or more pieces of output in a strictly mathematical fashion. While a rule-based planning algorithm, for example, would not go into (or at least could recognize) an invalid state, this is not true with statistical functions.Although the new approach offers solutions to problems that previously were too complex to consider or wouldn't have justified the high development cost, now we must critically evaluate the value of each model. Not just once, but regularly and repeatedly during the entire lifetime of the model, because the input data might imperceptibly change from useful to garbage (with corresponding garbage results).
In some situations, there might not be a sufficient model. Maybe the task is simply impossible, or no input data is provided, or the model does not have enough degrees of freedom to represent all the nuances. The algorithms to produce the models will usually terminate and present a result. Whether the model is useful must be determined afterwards.
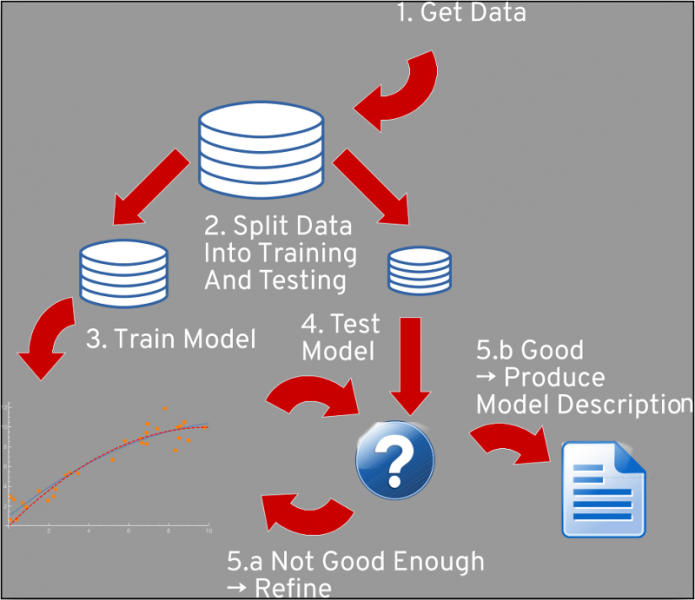
Scientific method of model development
The problems of model development are nothing new. Many generations of scientists have developed a rigorous approach to tackling a problem with an unknown solution and, ideally, without bias:- State a hypothesis for a given problem.
- Collect data that can be used as inputs to the model and for which the answers are known.
- Determine how much the model and the expected results match.
- If it's not good enough, return to #1.
The selection of a model's statistics and parameters is like creating a hypothesis. Most methods have a few parameters that can be freely and independently chosen, creating a possibly unlimited search space. On the other hand, there's a lot of compute power, and there's a finite number of methods that could test many different models at the same time.
Input data must be collected ahead of time for two purposes:
- training the model
- testing the model
First, the training data is applied to the model. If each input dataset record is associated with an expected result, we talk about a supervised learning problem, in which we try to discover a function that allows a target value to be computed from a set of input values that can be measured about an entity. (The measured data is the "input dataset record," and the target is the expected result.) If the output value is one of a given set, we talk about a classification problem. If the output is real-valued, we look at a regression problem. Otherwise it is unsupervised, meaning we have data and no specific goal or target.
After the model is trained, then it must be validated with the testing data. The model is applied to the inputs from the training dataset. In the case of a supervised learning problem, the results are compared with the available results from the testing set, and the match is measured. In the case of an unsupervised method, we must find other ways to evaluate the "correctness" of the model.
In the end, we get a score for the current model predicated on the currently available dataset. Then we can decide whether the model is good enough and we can use it (we call this inference) or whether to start again and develop a new model, perhaps with new parameters.
Requirements and limitations
It sounds easy enough to follow this recipe, especially since computers are supposed to do the heavy lifting. But there is no silver bullet, not even a guarantee of a solution. Successfully using machine learning requires a few things:- Choosing a method/algorithm appropriate for the problem
- Narrowing the search to account for the (usually) huge search space for the model's parameter
- Evaluating the model's precision, especially when automating the search
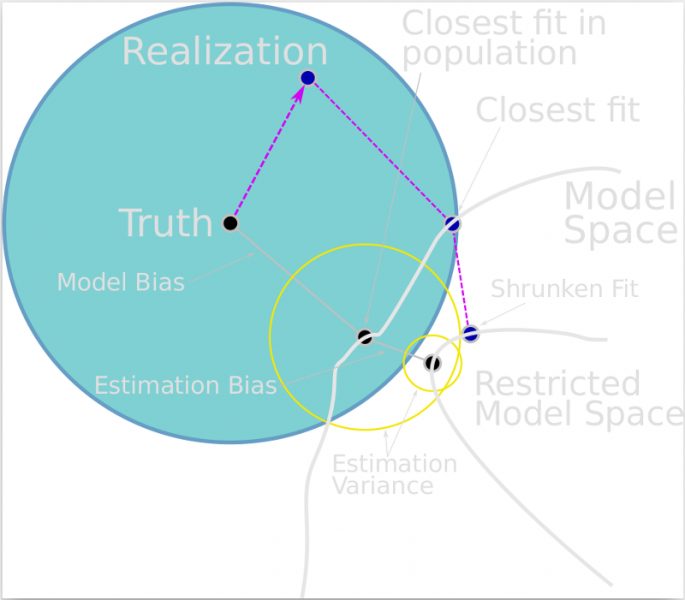
In addition, it's unrealistic to expect a model to find a 100% match with the observed data. There are just too many limitations in place, such as:
Other limitations include:
- The actual events or "things" likely don't match the ideal, blueprint solution.
- The events or things that are observed can be measured with limited precision.
- The model isn't built with all the necessary inputs that influence the real system, maybe because they can't (or can't realistically) be measured (e.g., the butterfly effect).
- Compromises must be made in the search, or the search must be terminated early, because the parameters' search space is too large.
Let's do the math
Let's start with simple methods. Hopefully you remember linear regression and logistic regression (the latter is the classification version) from your school days. The methods require the inputs to be available in numeric form (i.e., translate class data into vectors with a single non-zero entry) and consist of finding the optimal polynomial of a given degree to match the expected result. Efficient methods for the calculation are known, and it's possible to interpret the resulting model—at least to some degree. With extensions like lasso and ridge, you can even search for a simpler model that might behave less violently to unexpected inputs.At a similar level of intuitiveness are algorithms to look for similarities. Given that we can measure the "distance" between two datasets, we can use the k-nearest neighbor (kNN) method to cluster similar dataset records together. The algorithm does not need to know how many clusters we are looking for, and it works (though it's more unstable) with high-dimensional data. This is an unsupervised method and does not require any value to be computed from the input data. The input dataset is the data that's used.
Decision trees are also simple to use and interpret. They are mostly useful for classification problems, but with some limitations, could be used for regression as well. They work by splitting the remaining set of inputs into two pieces at every step along one dimension of the value. Afterwards, ideally one or both sides of the split contain only values of the same class (only cats, only dogs, only pudding). If this is not possible, at least the sets of data points on each side of the split are more "pure."
The process is repeated until the sets are pure (trivially possible if the set has just one element) or the resulting tree exceeds a depth limit. The resulting model is used by testing a new data element according to each split, down to the leaf of the tree, then it adopts as the answer the majority result of the remaining set in that leaf. Such a model can be easily translated into human languages as a cascade of if-then-else statements.
What about neural networks?
The news about machine learning is dominated by neural networks (NNs), and deep learning specifically. NNs are not new; they were an integral part of the last big revival of AI, but in the late '80s/early '90s, no one thought about making them as complex as they are today because the implementation would have been unrealistic.Inference using NNs is simple: the input is applied as a vector. There is a possibly large set of internal "neuron layers," which receive their inputs from the previous layer (or the inputs), and produce results for the next layer (or the output). Each neuron can take all or a subset of the values from the previous layer, scale each value with a factor, and then add up all the values. Then a constant value is added to make the method more general.
This operation can be expressed as simple vector-matrix multiplication. Performing all the operations for a layer at once is a tensor multiplication. The resulting scalar value is then optionally applied to a function that tries to create a binary output (0/1 or 1/-1). The sigmoid or ArcTanh functions are usually used. Repeat the process until the end, when a custom method can be used to determine the result from the output value or values of the last layer. NNs are particularly good at classification, but can be used for regression too.
The tricky part is how to construct the matrices representing the steps from one layer to the next. We have many input dataset records for which NNs can be evaluated. Maybe we could even compute a constellation of the matrices that would result in the exact right value for one input dataset record. But this computation would most likely invalidate similar steps we had done to match other records. There is no closed formula to compute the right values. A gradual learning approach is needed, where all dataset records are looked at repeatedly, each time the difference from the expected result is computed, and then a small step toward correcting the mistake is made (via a method called gradient descent).
We've created many variants of NNs that are good at different tasks. Convolutional NNs (CNNs) are good at handling pictures. Convolution can isolate features, regardless of their position or even orientation. Whether the cat is in the lower right or upper left part of the picture does not matter to a CNN.
Recurring NNs (RNNs) are good for temporal problems. Predicting time series (and anomaly detection), simulating long term vs. short term memory, and similar tasks can be implemented with RNNs.
Independent from these broad categories are methods to improve learning speed, improve the scale of problems that can be solved, or speed the time to train the system. For the latter, there are ways to construct NNs so they don't require tagged training data and become unsupervised algorithms.
Companies like Google, Facebook, LinkedIn, and Amazon have built their business models on these algorithms.
Not to be confused with optimization
Many people say AI or ML when they are really talking about optimization. It might seem like intelligence when an optimization algorithm finds a novel solution, but this is not really AI. Optimization algorithms are often used in the implementation of machine learning techniques.Convex optimization problems are straightforward search problems. Implementations differ in speed and in the requirements on the data provided, but, by definition, they are able to find the solution. Non-convex optimization problems can be solved probabilistically; this is perhaps where the confusion comes from. Nevertheless, optimizations are different from AI/ML. They are prevalent in the business world and most of those problems likely can be solved by optimization.
Learn more
AI/ML isn't the exclusive domain of data scientists; everyone—people with an idea, subject matter experts who can help interpret raw data, people who know where to find the data and wrangle it into shape (e.g., data engineers), anyone who simply feels inspired to learn data science—can work with data science experts and contribute to AI/ML.How are you using open source tools in your machine learning or AI projects? Send an article proposal to open@opensource.com.

No comments:
Post a Comment